Next: Eddy Induced Velocity (traadv_eiv, Up: Lateral Ocean Physics (LDF) Previous: Lateral Mixing Coefficient (ldftra, Contents Index
A direction for lateral mixing has to be defined when the desired operator does
not act along the model levels. This occurs when ![]() horizontal mixing is
required on tracer or momentum (ln_traldf_hor or ln_dynldf_hor)
in
horizontal mixing is
required on tracer or momentum (ln_traldf_hor or ln_dynldf_hor)
in ![]() - or mixed
- or mixed ![]() -
-![]() - coordinates, and
- coordinates, and ![]() isoneutral mixing is required
whatever the vertical coordinate is. This direction of mixing is defined by its
slopes in the i- and j-directions at the face of the cell of the
quantity to be diffused. For a tracer, this leads to the following four slopes :
isoneutral mixing is required
whatever the vertical coordinate is. This direction of mixing is defined by its
slopes in the i- and j-directions at the face of the cell of the
quantity to be diffused. For a tracer, this leads to the following four slopes :
![]() ,
, ![]() ,
, ![]() ,
, ![]() (see (5.9)), while
for momentum the slopes are
(see (5.9)), while
for momentum the slopes are ![]() ,
, ![]() ,
, ![]() ,
, ![]() for
for
![]() and
and ![]() ,
, ![]() ,
, ![]() ,
, ![]() for
for 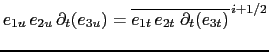 .
.
In ![]() -coordinates, geopotential mixing (
-coordinates, geopotential mixing (![]() horizontal mixing)
horizontal mixing) ![]() and
and
![]() are the slopes between the geopotential and computational surfaces.
Their discrete formulation is found by locally solving (5.9)
when the diffusive fluxes in the three directions are set to zero and
are the slopes between the geopotential and computational surfaces.
Their discrete formulation is found by locally solving (5.9)
when the diffusive fluxes in the three directions are set to zero and ![]() is
assumed to be horizontally uniform,
is
assumed to be horizontally uniform, ![]() a linear function of
a linear function of ![]() , the
depth of a
, the
depth of a ![]() -point.
-point.
These slopes are computed once in ldfslp_init when ln_sco=True, and either ln_traldf_hor=True or ln_dynldf_hor=True.
As the mixing is performed along neutral surfaces, the gradient of ![]() in
(9.11) has to be evaluated at the same local pressure (which,
in decibars, is approximated by the depth in meters in the model). Therefore
(9.11) cannot be used as such, but further transformation is
needed depending on the vertical coordinate used:
in
(9.11) has to be evaluated at the same local pressure (which,
in decibars, is approximated by the depth in meters in the model). Therefore
(9.11) cannot be used as such, but further transformation is
needed depending on the vertical coordinate used:
Note: The solution for ![]() -coordinate passes trough the use of different
(and better) expression for the constraint on iso-neutral fluxes. Following
Griffies [2004], instead of specifying directly that there is a zero neutral
diffusive flux of locally referenced potential density, we stay in the
-coordinate passes trough the use of different
(and better) expression for the constraint on iso-neutral fluxes. Following
Griffies [2004], instead of specifying directly that there is a zero neutral
diffusive flux of locally referenced potential density, we stay in the ![]() -
-![]() plane and consider the balance between the neutral direction diffusive fluxes
of potential temperature and salinity:
plane and consider the balance between the neutral direction diffusive fluxes
of potential temperature and salinity:
| (9.12) |
This constraint leads to the following definition for the slopes:
Note that such a formulation could be also used in the ![]() -coordinate and
-coordinate and
![]() -coordinate with partial steps cases.
-coordinate with partial steps cases.
This implementation is a rather old one. It is similar to the one
proposed by Cox [1987], except for the background horizontal
diffusion. Indeed, the Cox implementation of isopycnal diffusion in
GFDL-type models requires a minimum background horizontal diffusion
for numerical stability reasons. To overcome this problem, several
techniques have been proposed in which the numerical schemes of the
ocean model are modified [Weaver and Eby, 1997, Griffies et al., 1998]. Griffies's scheme is now available in NEMO if
traldf_grif_iso is set true; see Appdx D. Here,
another strategy is presented [Lazar, 1997]: a local
filtering of the iso-neutral slopes (made on 9 grid-points) prevents
the development of grid point noise generated by the iso-neutral
diffusion operator (Fig. 9.1). This allows an
iso-neutral diffusion scheme without additional background horizontal
mixing. This technique can be viewed as a diffusion operator that acts
along large-scale (2 ![]() x) iso-neutral surfaces. The diapycnal diffusion required
for numerical stability is thus minimized and its net effect on the
flow is quite small when compared to the effect of an horizontal
background mixing.
x) iso-neutral surfaces. The diapycnal diffusion required
for numerical stability is thus minimized and its net effect on the
flow is quite small when compared to the effect of an horizontal
background mixing.
Nevertheless, this iso-neutral operator does not ensure that variance cannot increase, contrary to the Griffies et al. [1998] operator which has that property.
For numerical stability reasons [Griffies, 2004, Cox, 1987], the slopes must also
be bounded by ![]() everywhere. This constraint is applied in a piecewise linear
fashion, increasing from zero at the surface to
everywhere. This constraint is applied in a piecewise linear
fashion, increasing from zero at the surface to ![]() at
at ![]() metres and thereafter
decreasing to zero at the bottom of the ocean. (the fact that the eddies "feel" the
surface motivates this flattening of isopycnals near the surface).
metres and thereafter
decreasing to zero at the bottom of the ocean. (the fact that the eddies "feel" the
surface motivates this flattening of isopycnals near the surface).
![\includegraphics[width=0.70\textwidth]{Fig_eiv_slp}](img892.png)
|
yellowadd here a discussion about the flattening of the slopes, vs tapering the coefficient.
The iso-neutral diffusion operator on momentum is the same as the one used on
tracers but applied to each component of the velocity separately (see
(6.27) in section 6.6.2). The slopes between the
surface along which the diffusion operator acts and the surface of computation
(![]() - or
- or ![]() -surfaces) are defined at
-surfaces) are defined at ![]() -,
-, ![]() -, and uw- points for the
-, and uw- points for the
![]() -component, and
-component, and ![]() -,
-, ![]() - and vw- points for the
- and vw- points for the 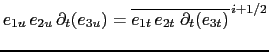 -component.
They are computed from the slopes used for tracer diffusion,
-component.
They are computed from the slopes used for tracer diffusion, ![]() (9.10) and (9.11) :
(9.10) and (9.11) :
The major issue remaining is in the specification of the boundary conditions. The same boundary conditions are chosen as those used for lateral diffusion along model level surfaces, i.e. using the shear computed along the model levels and with no additional friction at the ocean bottom (see §8.1).
Gurvan Madec and the NEMO Team
NEMO European Consortium2017-02-17