Boundary Condition at the Coast (rn_shlat)

!-----------------------------------------------------------------------
&namlbc        !   lateral momentum boundary condition
!-----------------------------------------------------------------------
   rn_shlat    =    2.     !  shlat = 0  !  0 < shlat < 2  !  shlat = 2  !  2 < shlat
                           !  free slip  !   partial slip  !   no slip   ! strong slip
   ln_vorlat   = .false.   !  consistency of vorticity boundary condition with analytical eqs.
/

Options are defined through the namlbc namelist variables. The discrete representation of a domain with complex boundaries (coastlines and bottom topography) leads to arrays that include large portions where a computation is not required as the model variables remain at zero. Nevertheless, vectorial supercomputers are far more efficient when computing over a whole array, and the readability of a code is greatly improved when boundary conditions are applied in an automatic way rather than by a specific computation before or after each computational loop. An efficient way to work over the whole domain while specifying the boundary conditions, is to use multiplication by mask arrays in the computation. A mask array is a matrix whose elements are $1$ in the ocean domain and 0 elsewhere. A simple multiplication of a variable by its own mask ensures that it will remain zero over land areas. Since most of the boundary conditions consist of a zero flux across the solid boundaries, they can be simply applied by multiplying variables by the correct mask arrays, $i.e.$ the mask array of the grid point where the flux is evaluated. For example, the heat flux in the i-direction is evaluated at $u$-points. Evaluating this quantity as,

$$\frac{A^{lT} }{e_1 }\frac{\partial T}{\partial i}\equiv \frac{A_u^{lT} }{e_{1u} } \; \delta _{i+1 / 2} \left[ T \right]\;\;mask_u$$ (8.1)

(where mask$_{u}$ is the mask array at a $u$-point) ensures that the heat flux is zero inside land and at the boundaries, since mask$_{u}$ is zero at solid boundaries which in this case are defined at $u$-points (normal velocity $u$ remains zero at the coast) (Fig. 8.1).

Figure 8.1: Lateral boundary (thick line) at T-level. The velocity normal to the boundary is set to zero.

For momentum the situation is a bit more complex as two boundary conditions must be provided along the coast (one each for the normal and tangential velocities). The boundary of the ocean in the C-grid is defined by the velocity-faces. For example, at a given $T$-level, the lateral boundary (a coastline or an intersection with the bottom topography) is made of segments joining $f$-points, and normal velocity points are located between two $f-$points (Fig. 8.1). The boundary condition on the normal velocity (no flux through solid boundaries) can thus be easily implemented using the mask system. The boundary condition on the tangential velocity requires a more specific treatment. This boundary condition influences the relative vorticity and momentum diffusive trends, and is required in order to compute the vorticity at the coast. Four different types of lateral boundary condition are available, controlled by the value of the rn_shlat namelist parameter. (The value of the mask$_{f}$ array along the coastline is set equal to this parameter.) These are:

Figure 8.2: lateral boundary condition (a) free-slip ( $rn\_shlat=0$) ; (b) no-slip ( $rn\_shlat=2$) ; (c) "partial" free-slip ( $0<rn\_shlat<2$) and (d) "strong" no-slip ( $2<rn\_shlat$). Implied "ghost" velocity inside land area is display in grey.

free-slip boundary condition (rn_shlat=0):

the tangential velocity at the coastline is equal to the offshore velocity, $i.e.$ the normal derivative of the tangential velocity is zero at the coast, so the vorticity: mask$_{f}$ array is set to zero inside the land and just at the coast (Fig. 8.2-a).

no-slip boundary condition (rn_shlat=2):

the tangential velocity vanishes at the coastline. Assuming that the tangential velocity decreases linearly from the closest ocean velocity grid point to the coastline, the normal derivative is evaluated as if the velocities at the closest land velocity gridpoint and the closest ocean velocity gridpoint were of the same magnitude but in the opposite direction (Fig. 8.2-b). Therefore, the vorticity along the coastlines is given by:

$$\zeta \equiv 2 \left(\delta_{i+1/2} \left[e_{2v} v \right] - \delta_{j+1/2} \left[e_{1u} u \right] \right) / \left(e_{1f} e_{2f} \right) ,$$

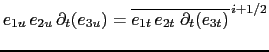where $u$ and $v$ are masked fields. Setting the mask$_{f}$ array to $2$ along the coastline provides a vorticity field computed with the no-slip boundary condition, simply by multiplying it by the mask$_{f}$ :

$$\zeta \equiv \frac{1}{e_{1f} {\kern 1pt}e_{2f} }\left( {\delta _{... ...ft[ {e_{2v} v} \right]-\delta _{j+1/2} \left[ {e_{1u} u} \right]} \right)\; _f$$ (8.2)

"partial" free-slip boundary condition (0$<$rn_shlat$<$2):

the tangential velocity at the coastline is smaller than the offshore velocity, $i.e.$ there is a lateral friction but not strong enough to make the tangential velocity at the coast vanish (Fig. 8.2-c). This can be selected by providing a value of mask$_{f}$ strictly inbetween 0 and $2$.

"strong" no-slip boundary condition (2$<$rn_shlat):

the viscous boundary layer is assumed to be smaller than half the grid size (Fig. 8.2-d). The friction is thus larger than in the no-slip case.

Note that when the bottom topography is entirely represented by the $s$-coor-dinates (pure $s$-coordinate), the lateral boundary condition on tangential velocity is of much less importance as it is only applied next to the coast where the minimum water depth can be quite shallow.

The alternative numerical implementation of the no-slip boundary conditions for an arbitrary coast line of Shchepetkin and O'Brien [1996] is also available through the key_ noslip_accurate CPP key. It is based on a fourth order evaluation of the shear at the coast which, in turn, allows a true second order scheme in the interior of the domain ($i.e.$ the numerical boundary scheme simulates the truncation error of the numerical scheme used in the interior of the domain). Shchepetkin and O'Brien [1996] found that such a technique considerably improves the quality of the numerical solution. In NEMO, such spectacular improvements have not been found in the half-degree global ocean (ORCA05), but significant reductions of numerically induced coastal upwellings were found in an eddy resolving simulation of the Alboran Sea [Olivier, 2001]. Nevertheless, since a no-slip boundary condition is not recommended in an eddy permitting or resolving simulation [Penduff et al., 2007], the use of this option is also not recommended.

In practice, the no-slip accurate option changes the way the curl is evaluated at the coast (see divcur.F90 module), and requires the nature of each coastline grid point (convex or concave corners, straight north-south or east-west coast) to be specified. This is performed in routine dom_msk_nsa in the domask.F90 module.