Horizontal Derivative in zps-coordinate (zpshde.F90)

With partial cells (ln_zps=true) at bottom and top (ln_isfcav=true), in general, tracers in horizontally adjacent cells live at different depths. Horizontal gradients of tracers are needed for horizontal diffusion (traldf.F90 module) and for the hydrostatic pressure gradient (dynhpg.F90 module) to be active.

Before taking horizontal gradients between the tracers next to the bottom, a linear interpolation in the vertical is used to approximate the deeper tracer as if it actually lived at the depth of the shallower tracer point (Fig. 5.5). For example, for temperature in the $i$-direction the needed interpolated temperature, $\widetilde{T}$, is:

Figure 5.5: Discretisation of the horizontal difference and average of tracers in the $z$-partial step coordinate (ln_zps=true) in the case $( e3w_k^{i+1} - e3w_k^i )>0$. A linear interpolation is used to estimate $\widetilde{T}_k^{i+1}$, the tracer value at the depth of the shallower tracer point of the two adjacent bottom $T$-points. The horizontal difference is then given by: $\delta _{i+1/2} T_k= \widetilde{T}_k^{ i+1} -T_k^{ i}$ and the average by: $\overline{T}_k^{ i+1/2}= ( \widetilde{T}_k^{ i+1/2} - T_k^{ i} ) / 2$.

$$\widetilde{T}= \left\{ \begin{aligned}&T^{ i+1} -\frac{ \left( e... ...k T^{i+1} && \quad\text{if $ e_{3w}^{i+1} < e_{3w}^i$ } \end{aligned} \right.$$

and the resulting forms for the horizontal difference and the horizontal average value of $T$ at a $U$-point are:

$$\begin{aligned}\delta _{i+1/2} T= \begin{cases} \widetilde... ...\text{if $ e_{3w}^{i+1} < e_{3w}^i$ } \end{cases} \end{aligned}$$

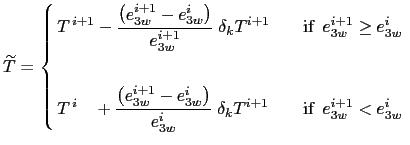The computation of horizontal derivative of tracers as well as of density is performed once for all at each time step in zpshde.F90 module and stored in shared arrays to be used when needed. It has to be emphasized that the procedure used to compute the interpolated density, $\widetilde{\rho }$, is not the same as that used for $T$ and $S$. Instead of forming a linear approximation of density, we compute $\widetilde{\rho }$ from the interpolated values of $T$ and $S$, and the pressure at a $u$-point (in the equation of state pressure is approximated by depth, see §5.8.1 ) :

$$\widetilde{\rho } = \rho ( {\widetilde{T},\widetilde {S},z_u }) z_u = \min \left( {z_T^{i+1} ,z_T^i } \right)$$ (5.29)

This is a much better approximation as the variation of $\rho$ with depth (and thus pressure) is highly non-linear with a true equation of state and thus is badly approximated with a linear interpolation. This approximation is used to compute both the horizontal pressure gradient (§6.4) and the slopes of neutral surfaces (§9.2)

Note that in almost all the advection schemes presented in this Chapter, both averaging and differencing operators appear. Yet (5.28) has not been used in these schemes: in contrast to diffusion and pressure gradient computations, no correction for partial steps is applied for advection. The main motivation is to preserve the domain averaged mean variance of the advected field when using the $2^{nd}$ order centred scheme. Sensitivity of the advection schemes to the way horizontal averages are performed in the vicinity of partial cells should be further investigated in the near future.

If under ice shelf seas opened (ln_isfcav=true), the partial cell properties at the top are computed in the same way as for the bottom. Some extra variables are, however, computed to reduce the flow generated at the top and bottom if $z*$ coordinates activated. The extra variables calculated and used by §6.4.4 are:

$\bullet$ $\overline{T}_k^{ i+1/2}$ as described in (5.28)

$\bullet$ $\delta _{i+1/2} Z_{T_k} = \widetilde {Z}^{ i}_{T_k}-Z^{ i}_{T_k}$ to compute the pressure gradient correction term used by (6.20) in §6.4.4, with $\widetilde {Z}_{T_k}$ the depth of the point $\widetilde {T}_{k}$ in case of $z^*$ coordinates (this term = 0 in z-coordinates)