Ocean Dynamics (DYN)

$$

Using the representation described in Chapter 4, several semi-discrete space forms of the dynamical equations are available depending on the vertical coordinate used and on the conservation properties of the vorticity term. In all the equations presented here, the masking has been omitted for simplicity. One must be aware that all the quantities are masked fields and that each time an average or difference operator is used, the resulting field is multiplied by a mask.

The prognostic ocean dynamics equation can be summarized as follows:

$$= \dbinom {\text{VOR} + \text{KEG} + \text {ZAD} } {\text{COR} + \text{ADV} } + \text{HPG} + \text{SPG} + \text{LDF} + \text{ZDF}$$

NXT stands for next, referring to the time-stepping. The first group of terms on the rhs of this equation corresponds to the Coriolis and advection terms that are decomposed into either a vorticity part (VOR), a kinetic energy part (KEG) and a vertical advection part (ZAD) in the vector invariant formulation, or a Coriolis and advection part (COR+ADV) in the flux formulation. The terms following these are the pressure gradient contributions (HPG, Hydrostatic Pressure Gradient, and SPG, Surface Pressure Gradient); and contributions from lateral diffusion (LDF) and vertical diffusion (ZDF), which are added to the rhs in the dynldf.F90 and dynzdf.F90 modules. The vertical diffusion term includes the surface and bottom stresses. The external forcings and parameterisations require complex inputs (surface wind stress calculation using bulk formulae, estimation of mixing coefficients) that are carried out in modules SBC, LDF and ZDF and are described in Chapters 7, 9 and 10, respectively.

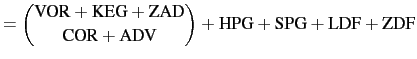In the present chapter we also describe the diagnostic equations used to compute the horizontal divergence, curl of the velocities (divcur module) and the vertical velocity (wzvmod module).

The different options available to the user are managed by namelist variables. For term ttt in the momentum equations, the logical namelist variables are ln_dynttt_xxx, where xxx is a 3 or 4 letter acronym corresponding to each optional scheme. If a CPP key is used for this term its name is key_ttt. The corresponding code can be found in the dynttt_xxx module in the DYN directory, and it is usually computed in the dyn_ttt_xxx subroutine.

The user has the option of extracting and outputting each tendency term from the 3D momentum equations (key_ trddyn defined), as described in Chap.15. Furthermore, the tendency terms associated with the 2D barotropic vorticity balance (when key_ trdvor is defined) can be derived from the 3D terms.

$$