Curvilinear z-coordinate System

Tensorial Formalism

In many ocean circulation problems, the flow field has regions of enhanced dynamics ($i.e.$ surface layers, western boundary currents, equatorial currents, or ocean fronts). The representation of such dynamical processes can be improved by specifically increasing the model resolution in these regions. As well, it may be convenient to use a lateral boundary-following coordinate system to better represent coastal dynamics. Moreover, the common geographical coordinate system has a singular point at the North Pole that cannot be easily treated in a global model without filtering. A solution consists of introducing an appropriate coordinate transformation that shifts the singular point onto land [Murray, 1996, Madec and Imbard, 1996]. As a consequence, it is important to solve the primitive equations in various curvilinear coordinate systems. An efficient way of introducing an appropriate coordinate transform can be found when using a tensorial formalism. This formalism is suited to any multidimensional curvilinear coordinate system. Ocean modellers mainly use three-dimensional orthogonal grids on the sphere (spherical earth approximation), with preservation of the local vertical. Here we give the simplified equations for this particular case. The general case is detailed by Eiseman and Stone [1980] in their survey of the conservation laws of fluid dynamics.

Let (i,j,k) be a set of orthogonal curvilinear coordinates on the sphere associated with the positively oriented orthogonal set of unit vectors (i,j,k) linked to the earth such that k is the local upward vector and (i,j) are two vectors orthogonal to k, $i.e.$ along geopotential surfaces (Fig.2.2). Let $(\lambda,\varphi,z)$ be the geographical coordinate system in which a position is defined by the latitude $\varphi(i,j)$, the longitude $\lambda(i,j)$ and the distance from the centre of the earth $a+z(k)$ where $a$ is the earth's radius and $z$ the altitude above a reference sea level (Fig.2.2). The local deformation of the curvilinear coordinate system is given by $e_1$, $e_2$ and $e_3$, the three scale factors:

$$\begin{aligned}e_1 &=\left( {a+z} \right)\;\left[ {\left( {\fra... ...&=\left( {\frac{\partial z}{\partial k}} \right) \end{aligned}$$

Figure 2.2: the geographical coordinate system $(\lambda,\varphi,z)$ and the curvilinear coordinate system (i,j,k).

Since the ocean depth is far smaller than the earth's radius, $a+z$, can be replaced by $a$ in (2.6) (thin-shell approximation). The resulting horizontal scale factors $e_1$, $e_2$ are independent of $k$ while the vertical scale factor is a single function of $k$ as k is parallel to z. The scalar and vector operators that appear in the primitive equations (Eqs. (2.1a) to (2.1f)) can be written in the tensorial form, invariant in any orthogonal horizontal curvilinear coordinate system transformation:

$$\begin{equation}\nabla q=\frac{1}{e_1 }\frac{\partial q}{\partial... ...ight) - \nabla \times \left( \nabla \times {\rm {\bf A}} \right) \end{equation}$$

where $q$ is a scalar quantity and ${\rm {\bf A}}=(a_1,a_2,a_3)$ a vector in the $(i,j,k)$ coordinate system.

Continuous Model Equations

In order to express the Primitive Equations in tensorial formalism, it is necessary to compute the horizontal component of the non-linear and viscous terms of the equation using (2.7a)) to (2.7e). Let us set $\vect U=(u,v,w)={\vect{U}}_h +w\;\vect{k}$, the velocity in the $(i,j,k)$ coordinate system and define the relative vorticity $\zeta$ and the divergence of the horizontal velocity field $\chi$, by:

$$\zeta =\frac{1}{e_1 e_2 }\left[ {\frac{\partial \left( {e_2 v} \right)}{\partial i}-\frac{\partial \left( {e_1 u} \right)}{\partial j}} \right]$$ (2.8)

$$\chi =\frac{1}{e_1 e_2 }\left[ {\frac{\partial \left( {e_2 u} \right)}{\partial i}+\frac{\partial \left( {e_1 v} \right)}{\partial j}} \right]$$ (2.9)

Using the fact that the horizontal scale factors $e_1$ and $e_2$ are independent of $k$ and that $e_3$ is a function of the single variable $k$, the nonlinear term of (2.1a) can be transformed as follows:

$$\left[ {\left( { \nabla \times {\rm {\bf U}} } \right) \times {\rm {\bf U}} +\frac{1}{2} \nabla \left( {{\rm {\bf U}}^2} \right)} \right]_h$$

$$\qquad=\left( {{\begin{array}{*{20}c} {\left[ { \frac{1}{e_3} \fr... ...rtial \left( u^2+v^2+w^2 \right)}{\partial j}} \hfill \end{array} }} \right)$$

$$\qquad =\left( {{ \begin{array}{*{20}c} {-\zeta \; v} \hfill {... ...\frac{1}{2e_2}\frac{\partial w^2}{\partial j}} \hfill \end{array} }} \right)$$

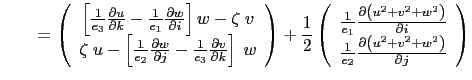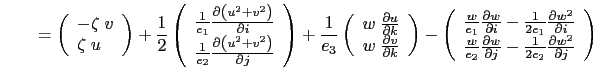The last term of the right hand side is obviously zero, and thus the nonlinear term of (2.1a) is written in the $(i,j,k)$ coordinate system:

$$\left[ {\left( { \nabla \times {\rm {\bf U}} } \right) \times {\r... ...f U}}_h^2 } \right)+\frac{1}{e_3 }w\frac{\partial {\rm {\bf U}}_h }{\partial k}$$ (2.10)

This is the so-called vector invariant form of the momentum advection term. For some purposes, it can be advantageous to write this term in the so-called flux form, $i.e.$ to write it as the divergence of fluxes. For example, the first component of (2.10) (the $i$-component) is transformed as follows:

$${ \begin{array}{*{20}l} \left[ {\left( {\nabla \times \vect{U}} \... ...+\frac{1}{e_3} \left( w\;\frac{\partial u}{\partial k} \right) \end{array} }$$

$${ \begin{array}{*{20}l} \qquad =\frac{1}{e_1 \; e_2} \left\{ -\le... ...right) }{\partial k} -u \frac{\partial w }{\partial k} \right) \end{array} }$$

$${ \begin{array}{*{20}l} \qquad =\frac{1}{e_1 \; e_2} \left( \frac... ...c{1}{e_1 e_2 }\left( -v^2\frac{\partial e_2 }{\partial i} \right) \end{array} }$$

$${ \begin{array}{*{20}l} \qquad = \nabla \cdot \left( {{\rm {\bf U... ... }{\partial i} +uv \frac{\partial e_1 }{\partial j} \right) \end{array} }$$

as $\nabla \cdot {\rm {\bf U}}\;=0$ (incompressibility) it comes:

$${ \begin{array}{*{20}l} \qquad = \nabla \cdot \left( {{\rm {\bf U... ...} -u \; \frac{\partial e_1}{\partial j} \right) \left( -v \right) \end{array} }$$

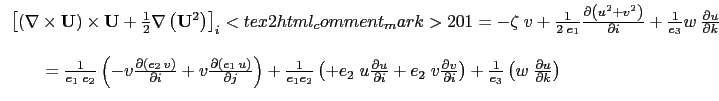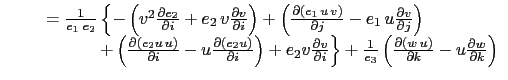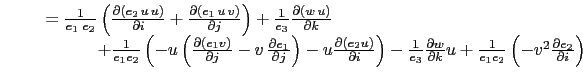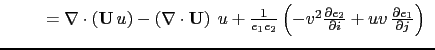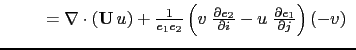The flux form of the momentum advection term is therefore given by:

$$\begin{multline} \left[ \left( {\nabla \times {\rm {\bf U}}} \right) \times {... ...l e_1}{\partial j} \right) {\rm {\bf k}} \times {\rm {\bf U}}_h \end{multline}$$

The flux form has two terms, the first one is expressed as the divergence of momentum fluxes (hence the flux form name given to this formulation) and the second one is due to the curvilinear nature of the coordinate system used. The latter is called the metric term and can be viewed as a modification of the Coriolis parameter:

$$f \to f + \frac{1}{e_1\;e_2} \left( v \frac{\partial e_2}{\partial i} -u \frac{\partial e_1}{\partial j} \right)$$ (2.11)

Note that in the case of geographical coordinate, $i.e.$ when $(i,j) \to (\lambda ,\varphi )$ and $(e_1 ,e_2) \to (a \cos \varphi ,a)$, we recover the commonly used modification of the Coriolis parameter $f \to f+(u/a) \tan \varphi$.

$$

To sum up, the curvilinear $z$-coordinate equations solved by the ocean model can be written in the following tensorial formalism:

$\bullet$ Vector invariant form of the momentum equations :

$$\begin{equation}\begin{split}\frac{\partial u}{\partial t} = + \l... ...{\rho _o} \right) &+ D_v^{\vect{U}} + F_v^{\vect{U}} \end{split} \end{equation}$$

$\bullet$ flux form of the momentum equations :

where $\zeta$, the relative vorticity, is given by (2.8) and $p_s$, the surface pressure, is given by:

$$p_s = \left\{ \begin{split}\rho g \eta & \qquad \qquad \; \... ...rtial t} \qquad \text{ filtered free surface} \end{split} \right.$$ (2.14)

with $\eta$ is solution of (2.5)

The vertical velocity and the hydrostatic pressure are diagnosed from the following equations:

$$\frac{\partial w}{\partial k}=-\chi \;e_3$$ (2.15)

$$\frac{\partial p_h }{\partial k}=-\rho \;g\;e_3$$ (2.16)

where the divergence of the horizontal velocity, $\chi$ is given by (2.9).

$\bullet$ tracer equations :

$$\frac{\partial T}{\partial t} = -\frac{1}{e_1 e_2 }\left[ { \frac... ...t] -\frac{1}{e_3 }\frac{\partial \left( {T w} \right)}{\partial k} + D^T + F^T$$ (2.17)

$$\frac{\partial S}{\partial t} = -\frac{1}{e_1 e_2 }\left[ {\frac{... ...t] -\frac{1}{e_3 }\frac{\partial \left( {S w} \right)}{\partial k} + D^S + F^S$$ (2.18)

$$\rho =\rho \left( {T,S,z(k)} \right)$$ (2.19)

The expression of D$^{U}$, $D^{S}$ and $D^{T}$ depends on the subgrid scale parameterisation used. It will be defined in §2.5.1. The nature and formulation of ${\rm {\bf F}}^{\rm {\bf U}}$, $F^T$ and $F^S$, the surface forcing terms, are discussed in Chapter 7.

$$