Discrete total energy conservation : flux form

Total energy conservation

The discrete form of the total energy conservation, (C.3), is given by:

$$\partial_t \left( \sum\limits_{i,j,k} \biggl\{ \frac{u^2}{2} b_u + \frac{v^2}{2} b_v + \rho g z_t b_t \biggr\} \right) =0$$

which in flux form, it leads to:

$$\sum\limits_{i,j,k} \biggl\{ \frac{u }{e_{3u}} \frac{\partial (e... ... b_u + \frac{v }{e_{3v}} \frac{\partial (e_{3v}v)}{\partial t} b_v \biggr\} - \frac{1}{2} \sum\limits_{i,j,k} \biggl\{ \frac{u^2}{e_{3u}}\fra... ...t} b_u + \frac{v^2}{e_{3v}}\frac{\partial e_{3v} }{\partial t} b_v \biggr\}$$

$$= - \sum\limits_{i,j,k} \biggl\{ \frac{1}{e_3t}\frac{\partial e_{... ...imits_{i,j,k} \biggl\{ \rho g \frac{\partial z_t}{\partial t} b_t \biggr\}$$

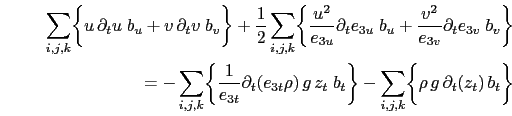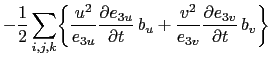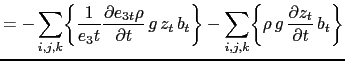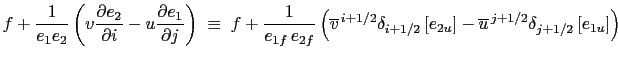Substituting the discrete expression of the time derivative of the velocity either in vector invariant or in flux form, leads to the discrete equivalent of the

Coriolis and advection terms: flux form

Coriolis plus “metric” Term

In flux from the vorticity term reduces to a Coriolis term in which the Coriolis parameter has been modified to account for the “metric” term. This altered Coriolis parameter is discretised at an f-point. It is given by:

$$f+\frac{1} {e_1 e_2 } \left( v \frac{\partial e_2 } {\partial i} ... ...2u} \right] -\overline u^{ j+1/2} \delta_{j+1/2} \left[ e_{1u} \right] \right)$$

Either the ENE or EEN scheme is then applied to obtain the vorticity term in flux form. It therefore conserves the total KE. The derivation is the same as for the vorticity term in the vector invariant form (§C.3.2).

Flux form advection

The flux form operator of the momentum advection is evaluated using a centered second order finite difference scheme. Because of the flux form, the discrete operator does not contribute to the global budget of linear momentum. Because of the centered second order scheme, it conserves the horizontal kinetic energy, that is :

$$- \int_D \textbf{U}_h \cdot \left( {{\begin{array}{*{20}c} \nabla... ...D { {\textbf{U}_h}^2 \frac{1}{e_3} \frac{\partial e_3 }{\partial t} \;dv } =\;0$$ (C.12)

Let us first consider the first term of the scalar product ($i.e.$ just the the terms associated with the i-component of the advection) :

$$- \int_D u \cdot \nabla \cdot \left( \textbf{U} u \right) \; dv$$

$$\equiv - \sum\limits_{i,j,k} \biggl\{ \frac{1} {b_u} \biggl( \delta_{i+1... ...ine {W}^{ i+1/2}\;\overline u^{ k+1/2} \right] \biggr) \; \biggr\} b_u \;u$$

$$\equiv - \sum\limits_{i,j,k} \biggl\{ \delta_{i+1/2} \left[ \overline {U... ...k \left[ \overline {W}^{ i+12}\;\overline u^{ k+1/2} \right] \; \biggr\} \; u$$

$$\equiv + \sum\limits_{i,j,k} \biggl\{ \overline {U}^{ i}\; \overline u^... ... {W}^{ i+1/2}\; \overline u^{ k+1/2} \delta_{k+1/2} \left[ u \right] \biggr\}$$

$$\equiv + \frac{1}{2} \sum\limits_{i,j,k} \biggl\{ \overline{U}^{ i} \de... ...u^2 \right] + \overline{W}^{ i+1/2} \delta_{k+1/2} \left[ u^2 \right] \biggr\}$$

$$\equiv - \sum\limits_{i,j,k} \frac{1}{2} \bigg\{ U \; \delta_{i+1/2} \le... ...,i} \right] + W \; \delta_{k+1/2} \left[ \overline {u^2}^{ i} \right] \biggr\}$$

$$\equiv - \sum\limits_{i,j,k} \frac{1}{2} \overline {u^2}^{ i} \biggl\{ ... ...t] + \delta_{j+1/2} \left[ V \right] + \delta_{k+1/2} \left[ W \right] \biggr\}$$

$$\equiv + \sum\limits_{i,j,k} \frac{1}{2} \overline {u^2}^{ i} \biggl\{ \left( \frac{1}{e_{3t}} \frac{\partial e_{3t}}{\partial t} \right) \; b_t \biggr\}$$

Applying similar manipulation applied to the second term of the scalar product leads to :

$$- \int_D \textbf{U}_h \cdot \left( {{\begin{array}{*{20}c} \nabla... ...ft( \frac{1}{e_{3t}} \frac{\partial e_{3t}}{\partial t} \right) \; b_t \biggr\}$$

which is the discrete form of $\frac{1}{2} \int_D u \cdot \nabla \cdot \left( \textbf{U} u \right) \; dv$. (C.12) is thus satisfied.

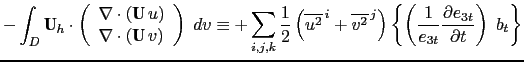When the UBS scheme is used to evaluate the flux form momentum advection, the discrete operator does not contribute to the global budget of linear momentum (flux form). The horizontal kinetic energy is not conserved, but forced to decay ($i.e.$ the scheme is diffusive).