Next: Discrete total energy conservation Up: Discrete Invariants of the Previous: Introduction / Notations Contents Index
The discretization of pimitive equation in ![]() -coordinate (
-coordinate (![]() time and space varying
vertical coordinate) must be chosen so that the discrete equation of the model satisfy
integral constrains on energy and enstrophy.
time and space varying
vertical coordinate) must be chosen so that the discrete equation of the model satisfy
integral constrains on energy and enstrophy.
Let us first establish those constraint in the continuous world.
The total energy (![]() kinetic plus potential energies) is conserved :
kinetic plus potential energies) is conserved :
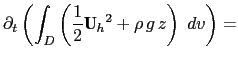 |
0 | (C.3) |
This equation can be transformed to obtain several sub-equalities. The transformation for the advection term depends on whether the vector invariant form or the flux form is used for the momentum equation. Using (C.2) and introducing (A.15) in (C.3) for the former form and Using (C.1) and introducing (A.16) in (C.3) for the latter form leads to:
where
![]() is the gradient along the
is the gradient along the ![]() -surfaces.
-surfaces.
blah blah....
![]()
The prognostic ocean dynamics equation can be summarized as follows:
NXT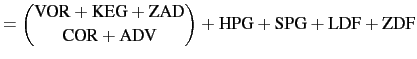 |
Vector invariant form:
Flux form:
![]()
(C.6c) is the balance between the conversion KE to PE and PE to KE. Indeed the left hand side of (C.6c) can be transformed as follows:
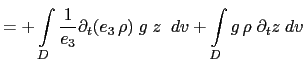 |
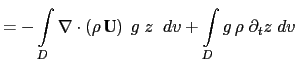 |
|
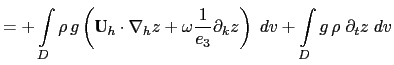 |
||
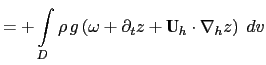 |
||
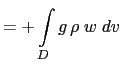 |
||
The left hand side of (C.6c) can be transformed as follows:
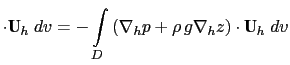 |
||
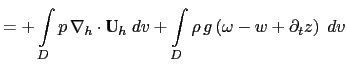 |
||
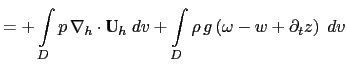 |
||
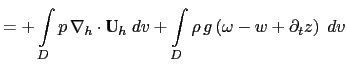 |
||
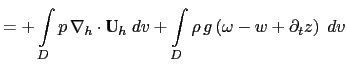 |
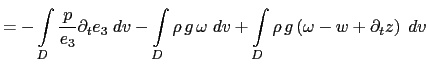 |
|
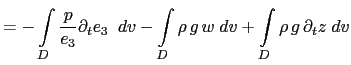 |
||
|
introducing the hydrostatic balance
| ||
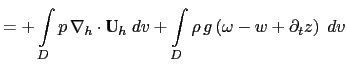 |
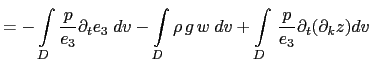 |
|
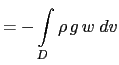 |
||
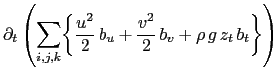 |
||
Gurvan Madec and the NEMO Team
NEMO European Consortium2017-02-17