Momentum Equation in $s-$coordinate

Here we only consider the first component of the momentum equation, the generalization to the second one being straightforward.

$$

$\bullet$ Total derivative in vector invariant form

Let us consider (2.13), the first component of the momentum equation in the vector invariant form. Its total $z-$coordinate time derivative, $\left. \frac{D u}{D t} \right\vert _z$ can be transformed as follows in order to obtain its expression in the curvilinear $s-$coordinate system:

Applying the time derivative chain rule (first equation of (A.2)) to $u$ and using (A.3) provides the expression of the last term of the right hand side,

$${\begin{array}{*{20}l} w_s \;\frac{\partial u}{\partial s} = \fra... ... - \left. {\frac{\partial u }{\partial t}} \right\vert _z \quad , \end{array} }$$

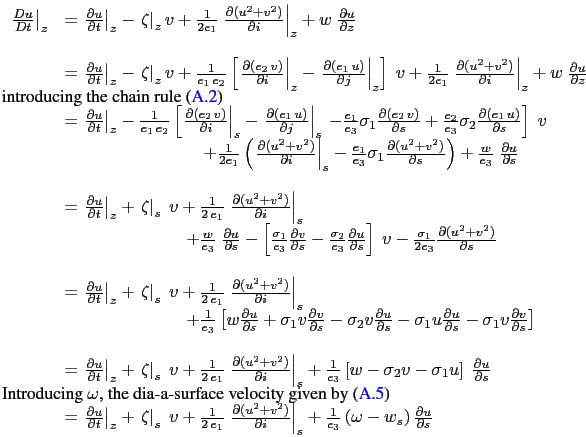leads to the $s-$coordinate formulation of the total $z-$coordinate time derivative, $i.e.$ the total $s-$coordinate time derivative :

$$\left. \frac{D u}{D t} \right\vert _s = \left. {\frac{\partial u ... ...tial i}} \right\vert _s + \frac{1}{e_3 } \omega \;\frac{\partial u}{\partial s}$$ (A.9)

Therefore, the vector invariant form of the total time derivative has exactly the same mathematical form in $z-$ and $s-$coordinates. This is not the case for the flux form as shown in next paragraph.

$$

$\bullet$ Total derivative in flux form

Let us start from the total time derivative in the curvilinear $s-$coordinate system we have just establish. Following the procedure used to establish (2.11), it can be transformed into :

$${\begin{array}{*{20}l} \left. \frac{D u}{D t} \right\vert _s &= \... ..._2 }{\partial i} -u \;\frac{\partial e_1 }{\partial j} \right) \end{array} }$$

Introducing the vertical scale factor inside the horizontal derivative of the first two terms ($i.e.$ the horizontal divergence), it becomes :

which leads to the $s-$coordinate flux formulation of the total $s-$coordinate time derivative, $i.e.$ the total $s-$coordinate time derivative in flux form :

$$\left. \frac{D u}{D t} \right\vert _s = \frac{1}{e_3} \left. \fra... ...;\frac{\partial e_2 }{\partial i} -u \;\frac{\partial e_1 }{\partial j} \right)$$ (A.11)

which is the total time derivative expressed in the curvilinear $s-$coordinate system. It has the same form as in the $z-$coordinate but for the vertical scale factor that has appeared inside the time derivative which comes from the modification of (A.7), the continuity equation.

$$

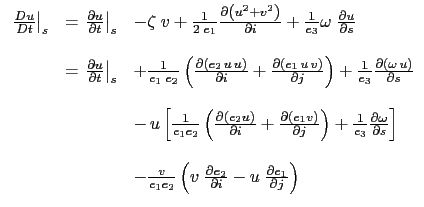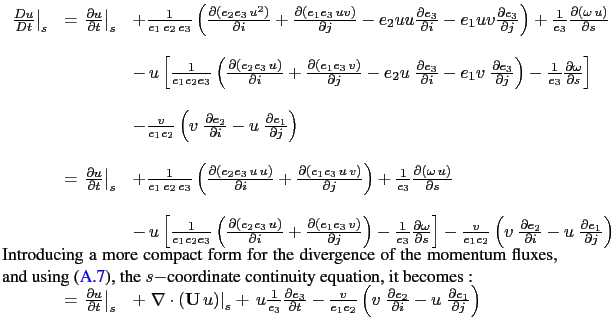$\bullet$ horizontal pressure gradient

The horizontal pressure gradient term can be transformed as follows:

$$\begin{split}-\frac{1}{\rho _o e_1 }\left. {\frac{\partial... ... \right\vert _s -\frac{g\;\rho }{\rho _o }\sigma _1 \end{split}$$

Applying similar manipulation to the second component and replacing $\sigma_1$ and $\sigma _2$ by their expression (A.1), it comes:

$$\begin{split}-\frac{1}{\rho _o e_1 } \left. {\frac{\partia... ...{\partial z}{\partial j}} \right\vert _s \right) \end{split}$$ (A.12)

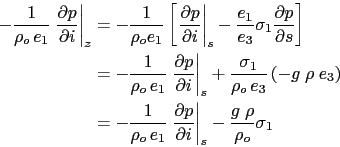An additional term appears in (A.14) which accounts for the tilt of $s-$surfaces with respect to geopotential $z-$surfaces.

As in $z$-coordinate, the horizontal pressure gradient can be split in two parts following Marsaleix et al. [2008]. Let defined a density anomaly, $d$, by $d=(\rho - \rho_o)/ \rho_o$, and a hydrostatic pressure anomaly, $p_h'$, by $p_h'= g \; \int_z^\eta d \; e_3 \; dk$. The pressure is then given by:

$$\begin{split}p &= g\; \int_z^\eta \rho \; e_3 \; dk = g\; \in... ..._z^\eta d \; e_3 \; dk + g \int_z^\eta e_3 \; dk \end{split}$$

Therefore, $p$ and $p_h'$ are linked through:

$$p = \rho_o \; p_h' + g ( z + \eta )$$ (A.13)

and the hydrostatic pressure balance expressed in terms of $p_h'$ and $d$ is:

$$\frac{\partial p_h'}{\partial k} = - d g e_3$$

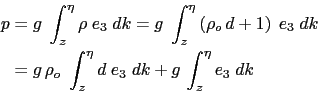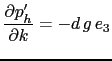Substituing (A.13) in (A.14) and using the definition of the density anomaly it comes the expression in two parts:

$$\begin{split}-\frac{1}{\rho _o e_1 } \left. {\frac{\partia... ...- \frac{g}{e_2 } \frac{\partial \eta}{\partial j} \end{split}$$ (A.14)

This formulation of the pressure gradient is characterised by the appearance of a term depending on the the sea surface height only (last term on the right hand side of expression (A.14)). This term will be loosely termed surface pressure gradient whereas the first term will be termed the hydrostatic pressure gradient by analogy to the $z$-coordinate formulation. In fact, the the true surface pressure gradient is $1/\rho_o \nabla (\rho \eta)$, and $\eta$ is implicitly included in the computation of $p_h'$ through the upper bound of the vertical integration.

$$

$\bullet$ The other terms of the momentum equation

The coriolis and forcing terms as well as the the vertical physics remain unchanged as they involve neither time nor space derivatives. The form of the lateral physics is discussed in appendix B.

$$

$\bullet$ Full momentum equation

To sum up, in a curvilinear $s$-coordinate system, the vector invariant momentum equation solved by the model has the same mathematical expression as the one in a curvilinear $z-$coordinate, except for the pressure gradient term :

whereas the flux form momentum equation differ from it by the formulation of both the time derivative and the pressure gradient term :

Both formulation share the same hydrostatic pressure balance expressed in terms of hydrostatic pressure and density anomalies, $p_h'$ and $d=( \frac{\rho}{\rho_o}-1 )$:

$$\frac{\partial p_h'}{\partial k} = - d g e_3$$ (A.17)

It is important to realize that the change in coordinate system has only concerned the position on the vertical. It has not affected (i,j,k), the orthogonal curvilinear set of unit vectors. ($u$,$v$) are always horizontal velocities so that their evolution is driven by horizontal forces, in particular the pressure gradient. By contrast, $\omega$ is not $w$, the third component of the velocity, but the dia-surface velocity component, $i.e.$ the volume flux across the moving $s$-surfaces per unit horizontal area.