Continuity Equation in $s-$coordinates

Using (A.2) and the fact that the horizontal scale factors $e_1$ and $e_2$ do not depend on the vertical coordinate, the divergence of the velocity relative to the ($i$,$j$,$z$) coordinate system is transformed as follows in order to obtain its expression in the curvilinear $s-$coordinate system:

Here, $w$ is the vertical velocity relative to the $z-$coordinate system. Introducing the dia-surface velocity component, $\omega$, defined as the volume flux across the moving $s$-surfaces per unit horizontal area:

$$\omega = w - w_s - \sigma _1 u - \sigma _2 v$$ (A.5)

with $w_s$ given by (A.3), we obtain the expression for the divergence of the velocity in the curvilinear $s-$coordinate system:

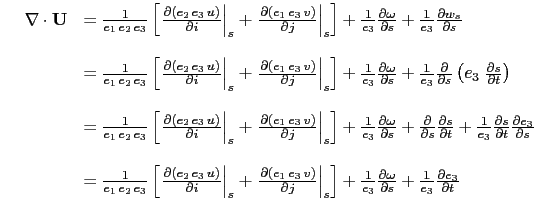As a result, the continuity equation (2.1c) in the $s-$coordinates is:

$$\frac{1}{e_3 } \frac{\partial e_3}{\partial t} + \frac{1}{e_1 e... ...\right\vert _s } \right] +\frac{1}{e_3 }\frac{\partial \omega }{\partial s} = 0$$ (A.7)

A additional term has appeared that take into account the contribution of the time variation of the vertical coordinate to the volume budget.