Next: Conservation Properties on Tracers Up: Discrete Invariants of the Previous: Discrete total energy conservation Contents Index
In the ENS scheme, the vorticity term is descretized as follows:
The scheme does not allow but the conservation of the total kinetic energy but the conservation
of ![]() , the potential enstrophy for a horizontally non-divergent flow (
, the potential enstrophy for a horizontally non-divergent flow (![]() when
when ![]() =0).
Indeed, using the symmetry or skew symmetry properties of the operators (Eqs (4.12)
and (4.11)), it can be shown that:
=0).
Indeed, using the symmetry or skew symmetry properties of the operators (Eqs (4.12)
and (4.11)), it can be shown that:
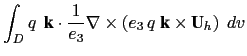 is the volume element. Indeed, using
(C.13), the discrete form of the right hand side of (C.14)
can be transformed as follow:
is the volume element. Indeed, using
(C.13), the discrete form of the right hand side of (C.14)
can be transformed as follow:
|
Since
| |||
![$\displaystyle \qquad {\begin{array}{*{20}l} &\equiv \sum\limits_{i,j,k} q \le...
...,j} \right] \right\} && \end{array} } \allowdisplaybreaks\allowdisplaybreaks$](img1617.png) |
|||
With the EEN scheme, the vorticity terms are represented as:
This formulation does conserve the potential enstrophy for a horizontally non-divergent flow (![]()
![]() ).
).
Let consider one of the vorticity triad, for example
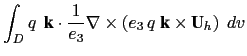 ,
similar manipulation can be done for the 3 others. The discrete form of the right hand
side of (C.14) applied to this triad only can be transformed as follow:
,
similar manipulation can be done for the 3 others. The discrete form of the right hand
side of (C.14) applied to this triad only can be transformed as follow:
Gurvan Madec and the NEMO Team
NEMO European Consortium2017-02-17