Domain: Vertical Grid (domzgr.F90 module)

!-----------------------------------------------------------------------
&namzgr        !   vertical coordinate
!-----------------------------------------------------------------------
   ln_zco      = .false.   !  z-coordinate - full    steps   (T/F)      ("key_zco" may also be defined)
   ln_zps      = .true.    !  z-coordinate - partial steps   (T/F)
   ln_sco      = .false.   !  s- or hybrid z-s-coordinate    (T/F)
   ln_isfcav   = .false.   !  ice shelf cavity               (T/F)
/

!-----------------------------------------------------------------------
&namdom        !   space and time domain (bathymetry, mesh, timestep)
!-----------------------------------------------------------------------
   nn_bathy    =    1      !  compute (=0) or read (=1) the bathymetry file
   rn_bathy    =    0.     !  value of the bathymetry. if (=0) bottom flat at jpkm1
   nn_closea   =    0      !  remove (=0) or keep (=1) closed seas and lakes (ORCA)
   nn_msh      =    1      !  create (=1) a mesh file or not (=0)
   rn_hmin     =   -3.     !  min depth of the ocean (>0) or min number of ocean level (<0)
   rn_e3zps_min=   20.     !  partial step thickness is set larger than the minimum of
   rn_e3zps_rat=    0.1    !  rn_e3zps_min and rn_e3zps_rat*e3t, with 0<rn_e3zps_rat<1
                           !
   rn_rdt      = 5760.     !  time step for the dynamics (and tracer if nn_acc=0)
   rn_atfp     =    0.1    !  asselin time filter parameter
   nn_acc      =    0      !  acceleration of convergence : =1      used, rdt < rdttra(k)
                                 !                          =0, not used, rdt = rdttra
   rn_rdtmin   = 28800.          !  minimum time step on tracers (used if nn_acc=1)
   rn_rdtmax   = 28800.          !  maximum time step on tracers (used if nn_acc=1)
   rn_rdth     =  800.           !  depth variation of tracer time step  (used if nn_acc=1)
   ln_crs      = .false.      !  Logical switch for coarsening module
   jphgr_msh   =       0               !  type of horizontal mesh
                                       !  = 0 curvilinear coordinate on the sphere read in coordinate.nc
                                       !  = 1 geographical mesh on the sphere with regular grid-spacing
                                       !  = 2 f-plane with regular grid-spacing
                                       !  = 3 beta-plane with regular grid-spacing
                                       !  = 4 Mercator grid with T/U point at the equator
   ppglam0     =       0.0             !  longitude of first raw and column T-point (jphgr_msh = 1)
   ppgphi0     =     -35.0             ! latitude  of first raw and column T-point (jphgr_msh = 1)
   ppe1_deg    =       1.0             !  zonal      grid-spacing (degrees)
   ppe2_deg    =       0.5             !  meridional grid-spacing (degrees)
   ppe1_m      =    5000.0             !  zonal      grid-spacing (degrees)
   ppe2_m      =    5000.0             !  meridional grid-spacing (degrees)
   ppsur       =    -4762.96143546300  !  ORCA r4, r2 and r05 coefficients
   ppa0        =      255.58049070440  ! (default coefficients)
   ppa1        =      245.58132232490  !
   ppkth       =       21.43336197938  !
   ppacr       =        3.0            !
   ppdzmin     =       10.             !  Minimum vertical spacing
   pphmax      =     5000.             !  Maximum depth
   ldbletanh   =    .TRUE.             !  Use/do not use double tanf function for vertical coordinates
   ppa2        =      100.760928500000 !  Double tanh function parameters
   ppkth2      =       48.029893720000 !
   ppacr2      =       13.000000000000 !
/

Variables are defined through the namzgr and namdom namelists. In the vertical, the model mesh is determined by four things: (1) the bathymetry given in meters ; (2) the number of levels of the model (jpk) ; (3) the analytical transformation $z(i,j,k)$ and the vertical scale factors (derivatives of the transformation) ; and (4) the masking system, $i.e.$ the number of wet model levels at each $(i,j)$ column of points.

Figure 4.5: The ocean bottom as seen by the model: (a) $z$-coordinate with full step, (b) $z$-coordinate with partial step, (c) $s$-coordinate: terrain following representation, (d) hybrid $s-z$ coordinate, (e) hybrid $s-z$ coordinate with partial step, and (f) same as (e) but with variable volume associated with the non-linear free surface. Note that the variable volume option (key_ vvl) can be used with any of the 5 coordinates (a) to (e).

The choice of a vertical coordinate, even if it is made through namzgr namelist parameters, must be done once of all at the beginning of an experiment. It is not intended as an option which can be enabled or disabled in the middle of an experiment. Three main choices are offered (Fig. 4.5a to c): $z$-coordinate with full step bathymetry (ln_zco = true), $z$-coordinate with partial step bathymetry (ln_zps = true), or generalized, $s$-coordinate (ln_sco = true). Hybridation of the three main coordinates are available: $s-z$ or $s-zps$ coordinate (Fig. 4.5d and 4.5e). When using the variable volume option key_ vvl ($i.e.$ non-linear free surface), the coordinate follow the time-variation of the free surface so that the transformation is time dependent: $z(i,j,k,t)$ (Fig. 4.5f). This option can be used with full step bathymetry or $s$-coordinate (hybrid and partial step coordinates have not yet been tested in NEMO v2.3). If using $z$-coordinate with partial step bathymetry (ln_zps = true), ocean cavity beneath ice shelves can be open (ln_isfcav = true) and partial step are also applied at the ocean/ice shelf interface.

Contrary to the horizontal grid, the vertical grid is computed in the code and no provision is made for reading it from a file. The only input file is the bathymetry (in meters) (bathy_meter.nc ). ^4.1. After reading the bathymetry, the algorithm for vertical grid definition differs between the different options:

zco

set a reference coordinate transformation $z_0 (k)$, and set $z(i,j,k,t)=z_0 (k)$.

zps

set a reference coordinate transformation $z_0 (k)$, and calculate the thickness of the deepest level at each $(i,j)$ point using the bathymetry, to obtain the final three-dimensional depth and scale factor arrays.

sco

smooth the bathymetry to fulfil the hydrostatic consistency criteria and set the three-dimensional transformation.

s-z and s-zps

smooth the bathymetry to fulfil the hydrostatic consistency criteria and set the three-dimensional transformation $z(i,j,k)$, and possibly introduce masking of extra land points to better fit the original bathymetry file

The arrays describing the grid point depths and vertical scale factors are three dimensional arrays $(i,j,k)$ even in the case of $z$-coordinate with full step bottom topography. In non-linear free surface (key_ vvl), their knowledge is required at before, now and after time step, while they do not vary in time in linear free surface case. To improve the code readability while providing this flexibility, the vertical coordinate and scale factors are defined as functions of $(i,j,k)$ with "fs" as prefix (examples: fse3t_b, fse3t_n, fse3t_a, for the before, now and after scale factors at $t$-point) that can be either three different arrays when key_ vvl is defined, or a single fixed arrays. These functions are defined in the file domzgr_substitute.h90 of the DOM directory. They are used throughout the code, and replaced by the corresponding arrays at the time of pre-processing (CPP capability).

Meter Bathymetry

Three options are possible for defining the bathymetry, according to the namelist variable nn_bathy (found in namdom namelist):

nn_bathy = 0

a flat-bottom domain is defined. The total depth $z_w (jpk)$ is given by the coordinate transformation. The domain can either be a closed basin or a periodic channel depending on the parameter jperio.

nn_bathy = -1

a domain with a bump of topography one third of the domain width at the central latitude. This is meant for the "EEL-R5" configuration, a periodic or open boundary channel with a seamount.

nn_bathy = 1

read a bathymetry and ice shelf draft (if needed). The bathy_meter.nc file (Netcdf format) provides the ocean depth (positive, in meters) at each grid point of the model grid. The bathymetry is usually built by interpolating a standard bathymetry product ($e.g.$ ETOPO2) onto the horizontal ocean mesh. Defining the bathymetry also defines the coastline: where the bathymetry is zero, no model levels are defined (all levels are masked).

The isfdraft_meter.nc file (Netcdf format) provides the ice shelf draft (positive, in meters) at each grid point of the model grid. This file is only needed if ln_isfcav = true. Defining the ice shelf draft will also define the ice shelf edge and the grounding line position.

When a global ocean is coupled to an atmospheric model it is better to represent all large water bodies (e.g, great lakes, Caspian sea...) even if the model resolution does not allow their communication with the rest of the ocean. This is unnecessary when the ocean is forced by fixed atmospheric conditions, so these seas can be removed from the ocean domain. The user has the option to set the bathymetry in closed seas to zero (see §15.2), but the code has to be adapted to the user's configuration.

$z$-coordinate (ln_zco=true) and reference coordinate

Figure: Default vertical mesh for ORCA2: 30 ocean levels (L30). Vertical level functions for (a) T-point depth and (b) the associated scale factor as computed from (4.14) using (4.15) in $z$-coordinate.

The reference coordinate transformation $z_0 (k)$ defines the arrays $gdept_0$ and $gdepw_0$ for $t$- and $w$-points, respectively. As indicated on Fig.4.3 jpk is the number of $w$-levels. $gdepw_0(1)$ is the ocean surface. There are at most jpk-1 $t$-points inside the ocean, the additional $t$-point at $jk=jpk$ is below the sea floor and is not used. The vertical location of $w$- and $t$-levels is defined from the analytic expression of the depth $z_0 (k)$ whose analytical derivative with respect to $k$ provides the vertical scale factors. The user must provide the analytical expression of both $z_0$ and its first derivative with respect to $k$. This is done in routine domzgr.F90 through statement functions, using parameters provided in the namcfg namelist.

It is possible to define a simple regular vertical grid by giving zero stretching (ppacr=0). In that case, the parameters jpk (number of $w$-levels) and pphmax (total ocean depth in meters) fully define the grid.

For climate-related studies it is often desirable to concentrate the vertical resolution near the ocean surface. The following function is proposed as a standard for a $z$-coordinate (with either full or partial steps):

$$\begin{split}z_0 (k) &= h_{sur} -h_0 \;k-\;h_1 \;\log \left[ ... ...ft( {{(k-h_{th} )} / {h_{cr} }} \right) \right\vert \end{split}$$ (4.12)

where $k=1$ to jpk for $w$-levels and $k=1$ to $k=1$ for $T-$levels. Such an expression allows us to define a nearly uniform vertical location of levels at the ocean top and bottom with a smooth hyperbolic tangent transition in between (Fig. 4.6).

If the ice shelf cavities are opened (ln_isfcav= true ), the definition of $z_0$ is the same. However, definition of $e_3^0$ at $t$- and $w$-points is respectively changed to:

$$\begin{split}e_3^T(k) &= z_W (k+1) - z_W (k) e_3^W(k) &= z_T (k) - z_T (k-1) \end{split}$$ (4.13)

This formulation decrease the self-generated circulation into the ice shelf cavity (which can, in extreme case, leads to blow up).

The most used vertical grid for ORCA2 has $10 m$ ($500 m)$ resolution in the surface (bottom) layers and a depth which varies from 0 at the sea surface to a minimum of $-5000 m$. This leads to the following conditions:

$$\begin{split}e_3 (1+1/2) &=10. e_3 (jpk-1/2) &=500. z(1) &=0. z(jpk) &=-5000. \end{split}$$ (4.14)

With the choice of the stretching $h_{cr} =3$ and the number of levels jpk=$31$, the four coefficients $h_{sur}$, $h_{0}$, $h_{1}$, and $h_{th}$ in (4.14) have been determined such that (4.15) is satisfied, through an optimisation procedure using a bisection method. For the first standard ORCA2 vertical grid this led to the following values: $h_{sur} =4762.96$, $h_0 =255.58, h_1 =245.5813$, and $h_{th} =21.43336$. The resulting depths and scale factors as a function of the model levels are shown in Fig. 4.6 and given in Table 4.2. Those values correspond to the parameters ppsur, ppa0, ppa1, ppkth in namcfg namelist.

Rather than entering parameters $h_{sur}$, $h_{0}$, and $h_{1}$ directly, it is possible to recalculate them. In that case the user sets ppsur=ppa0=ppa1=999999., in namcfg namelist, and specifies instead the four following parameters:

• ppacr=$h_{cr}$: stretching factor (nondimensional). The larger ppacr, the smaller the stretching. Values from $3$ to $10$ are usual.
• ppkth=$h_{th}$: is approximately the model level at which maximum stretching occurs (nondimensional, usually of order 1/2 or 2/3 of jpk)
• ppdzmin: minimum thickness for the top layer (in meters)
• pphmax: total depth of the ocean (meters).

As an example, for the $45$ layers used in the DRAKKAR configuration those parameters are: jpk=46, ppacr=9, ppkth=23.563, ppdzmin=6m, pphmax=5750m.

Table 4.2: Default vertical mesh in $z$-coordinate for 30 layers ORCA2 configuration as computed from (4.14) using the coefficients given in (4.15)

LEVEL	gdept	gdepw	e3t	e3w
1	5.00	0.00	10.00	10.00
2	15.00	10.00	10.00	10.00
3	25.00	20.00	10.00	10.00
4	35.01	30.00	10.01	10.00
5	45.01	40.01	10.01	10.01
6	55.03	50.02	10.02	10.02
7	65.06	60.04	10.04	10.03
8	75.13	70.09	10.09	10.06
9	85.25	80.18	10.17	10.12
10	95.49	90.35	10.33	10.24
11	105.97	100.69	10.65	10.47
12	116.90	111.36	11.27	10.91
13	128.70	122.65	12.47	11.77
14	142.20	135.16	14.78	13.43
15	158.96	150.03	19.23	16.65
16	181.96	169.42	27.66	22.78
17	216.65	197.37	43.26	34.30
18	272.48	241.13	70.88	55.21
19	364.30	312.74	116.11	90.99
20	511.53	429.72	181.55	146.43
21	732.20	611.89	261.03	220.35
22	1033.22	872.87	339.39	301.42
23	1405.70	1211.59	402.26	373.31
24	1830.89	1612.98	444.87	426.00
25	2289.77	2057.13	470.55	459.47
26	2768.24	2527.22	484.95	478.83
27	3257.48	3011.90	492.70	489.44
28	3752.44	3504.46	496.78	495.07
29	4250.40	4001.16	498.90	498.02
30	4749.91	4500.02	500.00	499.54
31	5250.23	5000.00	500.56	500.33

$z$-coordinate with partial step (ln_zps=.true.)

!-----------------------------------------------------------------------
&namdom        !   space and time domain (bathymetry, mesh, timestep)
!-----------------------------------------------------------------------
   nn_bathy    =    1      !  compute (=0) or read (=1) the bathymetry file
   rn_bathy    =    0.     !  value of the bathymetry. if (=0) bottom flat at jpkm1
   nn_closea   =    0      !  remove (=0) or keep (=1) closed seas and lakes (ORCA)
   nn_msh      =    1      !  create (=1) a mesh file or not (=0)
   rn_hmin     =   -3.     !  min depth of the ocean (>0) or min number of ocean level (<0)
   rn_e3zps_min=   20.     !  partial step thickness is set larger than the minimum of
   rn_e3zps_rat=    0.1    !  rn_e3zps_min and rn_e3zps_rat*e3t, with 0<rn_e3zps_rat<1
                           !
   rn_rdt      = 5760.     !  time step for the dynamics (and tracer if nn_acc=0)
   rn_atfp     =    0.1    !  asselin time filter parameter
   nn_acc      =    0      !  acceleration of convergence : =1      used, rdt < rdttra(k)
                                 !                          =0, not used, rdt = rdttra
   rn_rdtmin   = 28800.          !  minimum time step on tracers (used if nn_acc=1)
   rn_rdtmax   = 28800.          !  maximum time step on tracers (used if nn_acc=1)
   rn_rdth     =  800.           !  depth variation of tracer time step  (used if nn_acc=1)
   ln_crs      = .false.      !  Logical switch for coarsening module
   jphgr_msh   =       0               !  type of horizontal mesh
                                       !  = 0 curvilinear coordinate on the sphere read in coordinate.nc
                                       !  = 1 geographical mesh on the sphere with regular grid-spacing
                                       !  = 2 f-plane with regular grid-spacing
                                       !  = 3 beta-plane with regular grid-spacing
                                       !  = 4 Mercator grid with T/U point at the equator
   ppglam0     =       0.0             !  longitude of first raw and column T-point (jphgr_msh = 1)
   ppgphi0     =     -35.0             ! latitude  of first raw and column T-point (jphgr_msh = 1)
   ppe1_deg    =       1.0             !  zonal      grid-spacing (degrees)
   ppe2_deg    =       0.5             !  meridional grid-spacing (degrees)
   ppe1_m      =    5000.0             !  zonal      grid-spacing (degrees)
   ppe2_m      =    5000.0             !  meridional grid-spacing (degrees)
   ppsur       =    -4762.96143546300  !  ORCA r4, r2 and r05 coefficients
   ppa0        =      255.58049070440  ! (default coefficients)
   ppa1        =      245.58132232490  !
   ppkth       =       21.43336197938  !
   ppacr       =        3.0            !
   ppdzmin     =       10.             !  Minimum vertical spacing
   pphmax      =     5000.             !  Maximum depth
   ldbletanh   =    .TRUE.             !  Use/do not use double tanf function for vertical coordinates
   ppa2        =      100.760928500000 !  Double tanh function parameters
   ppkth2      =       48.029893720000 !
   ppacr2      =       13.000000000000 !
/

In $z$-coordinate partial step, the depths of the model levels are defined by the reference analytical function $z_0 (k)$ as described in the previous section, except in the bottom layer. The thickness of the bottom layer is allowed to vary as a function of geographical location $(\lambda,\varphi)$ to allow a better representation of the bathymetry, especially in the case of small slopes (where the bathymetry varies by less than one level thickness from one grid point to the next). The reference layer thicknesses $e_{3t}^0$ have been defined in the absence of bathymetry. With partial steps, layers from 1 to jpk-2 can have a thickness smaller than $e_{3t}(jk)$. The model deepest layer (jpk-1) is allowed to have either a smaller or larger thickness than $e_{3t}(jpk)$: the maximum thickness allowed is $2*e_{3t}(jpk-1)$. This has to be kept in mind when specifying values in namdom namelist, as the maximum depth pphmax in partial steps: for example, with pphmax$=5750 m$ for the DRAKKAR 45 layer grid, the maximum ocean depth allowed is actually $6000 m$ (the default thickness $e_{3t}(jpk-1)$ being $250 m$). Two variables in the namdom namelist are used to define the partial step vertical grid. The mimimum water thickness (in meters) allowed for a cell partially filled with bathymetry at level jk is the minimum of rn_e3zps_min (thickness in meters, usually $20 m$) or $e_{3t}(jk)*\textit{rn\_e3zps\_rat}\index{Namelist variables!rn\_e3zps\_rat}$ (a fraction, usually 10%, of the default thickness $e_{3t}(jk)$).

$s$-coordinate (ln_sco=true)

!-----------------------------------------------------------------------
&namzgr_sco    !   s-coordinate or hybrid z-s-coordinate
!-----------------------------------------------------------------------
   ln_s_sh94   = .true.    !  Song & Haidvogel 1994 hybrid S-sigma   (T)|
   ln_s_sf12   = .false.   !  Siddorn & Furner 2012 hybrid S-z-sigma (T)| if both are false the NEMO tanh stretching is applied
   ln_sigcrit  = .false.   !  use sigma coordinates below critical depth (T) or Z coordinates (F) for Siddorn & Furner stretch
                           !  stretching coefficients for all functions
   rn_sbot_min =   10.0    !  minimum depth of s-bottom surface (>0) (m)
   rn_sbot_max = 7000.0    !  maximum depth of s-bottom surface (= ocean depth) (>0) (m)
   rn_hc       =  150.0    !  critical depth for transition to stretched coordinates
                        !!!!!!!  Envelop bathymetry
   rn_rmax     =    0.3    !  maximum cut-off r-value allowed (0<r_max<1)
                        !!!!!!!  SH94 stretching coefficients  (ln_s_sh94 = .true.)
   rn_theta    =    6.0    !  surface control parameter (0<=theta<=20)
   rn_bb       =    0.8    !  stretching with SH94 s-sigma
                        !!!!!!!  SF12 stretching coefficient  (ln_s_sf12 = .true.)
   rn_alpha    =    4.4    !  stretching with SF12 s-sigma
   rn_efold    =    0.0    !  efold length scale for transition to stretched coord
   rn_zs       =    1.0    !  depth of surface grid box
                           !  bottom cell depth (Zb) is a linear function of water depth Zb = H*a + b
   rn_zb_a     =    0.024  !  bathymetry scaling factor for calculating Zb
   rn_zb_b     =   -0.2    !  offset for calculating Zb
                        !!!!!!!! Other stretching (not SH94 or SF12) [also uses rn_theta above]
   rn_thetb    =    1.0    !  bottom control parameter  (0<=thetb<= 1)
/

Options are defined in namzgr_sco. In $s$-coordinate (ln_sco = true), the depth and thickness of the model levels are defined from the product of a depth field and either a stretching function or its derivative, respectively:

$$\begin{split}z(k) &= h(i,j) \; z_0(k) e_3(k) &= h(i,j) \; z_0'(k) \end{split}$$ (4.15)

where $h$ is the depth of the last $w$-level ($z_0 (k)$) defined at the $t$-point location in the horizontal and $z_0 (k)$ is a function which varies from 0 at the sea surface to $1$ at the ocean bottom. The depth field $h$ is not necessary the ocean depth, since a mixed step-like and bottom-following representation of the topography can be used (Fig. 4.5d-e) or an envelop bathymetry can be defined (Fig. 4.5f). The namelist parameter rn_rmax determines the slope at which the terrain-following coordinate intersects the sea bed and becomes a pseudo z-coordinate. The coordinate can also be hybridised by specifying rn_sbot_min and rn_sbot_max as the minimum and maximum depths at which the terrain-following vertical coordinate is calculated.

Options for stretching the coordinate are provided as examples, but care must be taken to ensure that the vertical stretch used is appropriate for the application.

The original default NEMO s-coordinate stretching is available if neither of the other options are specified as true (ln_sco_SH94 = false and ln_sco_SF12 = false.) This uses a depth independent $\tanh$ function for the stretching [Madec et al., 1996]:

$$z = s_{min}+C\left(s\right)\left(H-s_{min}\right)$$ (4.16)

where $s_{min}$ is the depth at which the s-coordinate stretching starts and allows a z-coordinate to placed on top of the stretched coordinate, and z is the depth (negative down from the asea surface).

$$s = -\frac{k}{n-1} \quad 0 \leq k \leq n-1$$ (4.17)

$$\begin{split}C(s) &= \frac{ \left[ \tanh{ \left( \theta (s... ... \right)} \right]} {2\;\sinh \left( \theta \right)} \end{split}$$ (4.18)

A stretching function, modified from the commonly used Song and Haidvogel [1994] stretching (ln_sco_SH94 = true), is also available and is more commonly used for shelf seas modelling:

$$C\left(s\right) = \left(1 - b \right)\frac{ \sinh\left( \theta s\... ...t] - \tanh\left(\frac{\theta}{2}\right)}{ 2\tanh\left (\frac{\theta}{2}\right)}$$ (4.19)

Figure 4.7: Examples of the stretching function applied to a seamount; from left to right: surface, surface and bottom, and bottom intensified resolutions

where $H_c$ is the critical depth (rn_hc) at which the coordinate transitions from pure $\sigma$ to the stretched coordinate, and $\theta$ (rn_theta) and $b$ (rn_bb) are the surface and bottom control parameters such that $0\leqslant \theta \leqslant 20$, and $0\leqslant b\leqslant 1$. $b$ has been designed to allow surface and/or bottom increase of the vertical resolution (Fig. 4.7).

Another example has been provided at version 3.5 (ln_sco_SF12) that allows a fixed surface resolution in an analytical terrain-following stretching Siddorn and Furner [2012]. In this case the a stretching function $\gamma$ is defined such that:

$$z = -\gamma h \quad 0 \leq \gamma \leq 1$$ (4.20)

The function is defined with respect to $\sigma$, the unstretched terrain-following coordinate:

$$\gamma= A\left(\sigma-\frac{1}{2}\left(\sigma^{2}+f\left(\sigma\r... ...ight)\right)+B\left(\sigma^{3}-f\left(\sigma\right)\right)+f\left(\sigma\right)$$ (4.21)

Where:

$$f\left(\sigma\right)=\left(\alpha+2\right)\sigma^{\alpha+1}-\left(\alpha+1\right)\sigma^{\alpha+2} \quad \sigma = \frac{k}{n-1}$$ (4.22)

This gives an analytical stretching of $\sigma$ that is solvable in $A$ and $B$ as a function of the user prescribed stretching parameter $\alpha$ (rn_alpha) that stretches towards the surface ( $\alpha > 1.0$) or the bottom ( $\alpha < 1.0$) and user prescribed surface (rn_zs) and bottom depths. The bottom cell depth in this example is given as a function of water depth:

$$Z_b= h a + b$$ (4.23)

where the namelist parameters rn_zb_a and rn_zb_b are $a$ and $b$ respectively.

Figure 4.8: A comparison of the Song and Haidvogel [1994] $S$-coordinate (solid lines), a 50 level $Z$-coordinate (contoured surfaces) and the Siddorn and Furner [2012] $S$-coordinate (dashed lines) in the surface 100m for a idealised bathymetry that goes from 50m to 5500m depth. For clarity every third coordinate surface is shown.

This gives a smooth analytical stretching in computational space that is constrained to given specified surface and bottom grid cell thicknesses in real space. This is not to be confused with the hybrid schemes that superimpose geopotential coordinates on terrain following coordinates thus creating a non-analytical vertical coordinate that therefore may suffer from large gradients in the vertical resolutions. This stretching is less straightforward to implement than the Song and Haidvogel [1994] stretching, but has the advantage of resolving diurnal processes in deep water and has generally flatter slopes.

As with the Song and Haidvogel [1994] stretching the stretch is only applied at depths greater than the critical depth $h_c$. In this example two options are available in depths shallower than $h_c$, with pure sigma being applied if the ln_sigcrit is true and pure z-coordinates if it is false (the z-coordinate being equal to the depths of the stretched coordinate at $h_c$.

Minimising the horizontal slope of the vertical coordinate is important in terrain-following systems as large slopes lead to hydrostatic consistency. A hydrostatic consistency parameter diagnostic following Haney [1991] has been implemented, and is output as part of the model mesh file at the start of the run.

$z^*$- or $s^*$-coordinate (add key_ vvl)

This option is described in the Report by Levier et al. (2007), available on the NEMO web site.

level bathymetry and mask

Whatever the vertical coordinate used, the model offers the possibility of representing the bottom topography with steps that follow the face of the model cells (step like topography) [Madec et al., 1996]. The distribution of the steps in the horizontal is defined in a 2D integer array, mbathy, which gives the number of ocean levels ($i.e.$ those that are not masked) at each $t$-point. mbathy is computed from the meter bathymetry using the definiton of gdept as the number of $t$-points which gdept $\leq$ bathy.

Modifications of the model bathymetry are performed in the bat_ctl routine (see domzgr.F90 module) after mbathy is computed. Isolated grid points that do not communicate with another ocean point at the same level are eliminated.

As for the representation of bathymetry, a 2D integer array, misfdep, is created. misfdep defines the level of the first wet $t$-point. All the cells between $k=1$ and $misfdep(i,j)-1$ are masked. By default, misfdep(:,:)=1 and no cells are masked.

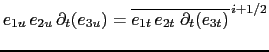In case of ice shelf cavities (ln_isfcav = true), modifications of the model bathymetry and ice shelf draft in the cavities are performed through the zgr_isf routine. The compatibility between ice shelf draft and bathymetry is checked: if only one cell on the water column is opened at $t$-, $u$- or $v$-points, the bathymetry or the ice shelf draft is dug to have a 2-level water column (i.e. two unmasked levels). If the incompatibility is too strong (i.e. need to dig more than one cell), the entire water column is masked.

From the mbathy array, the mask fields are defined as follows:

$$tmask(i,j,k) = \begin{cases}\; 0& \text{ if $k < misfdep(i,j) $ } \; 1& \t... ... \leq k\leq mbathy(i,j)$ } \; 0& \text{ if $k > mbathy(i,j)$ } \end{cases}$$

$$umask(i,j,k) = \; tmask(i,j,k) * tmask(i+1,j,k)$$

$$vmask(i,j,k) = \; tmask(i,j,k) * tmask(i,j+1,k)$$

$$fmask(i,j,k) = \; tmask(i,j,k) * tmask(i+1,j,k)$$

$$* tmask(i,j,k) * tmask(i+1,j,k)$$

$$wmask(i,j,k) = \; tmask(i,j,k) * tmask(i,j,k-1) wmask(i,j,1) = tmask(i,j,1)$$

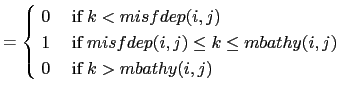Note, wmask is now defined. It allows, in case of ice shelves, to deal with the top boundary (ice shelf/ocean interface) exactly in the same way as for the bottom boundary.

The specification of closed lateral boundaries requires that at least the first and last rows and columns of the mbathy array are set to zero. In the particular case of an east-west cyclical boundary condition, mbathy has its last column equal to the second one and its first column equal to the last but one (and so too the mask arrays) (see § 8.2).

Footnotes

... files!bathy_meter.nc).^4.1

N.B. in full step $z$-coordinate, a bathy_level.nc file can replace the bathy_meter.nc file, so that the computation of the number of wet ocean point in each water column is by-passed