Conservation Properties on Lateral Momentum Physics

The discrete formulation of the horizontal diffusion of momentum ensures the conservation of potential vorticity and the horizontal divergence, and the dissipation of the square of these quantities ($i.e.$ enstrophy and the variance of the horizontal divergence) as well as the dissipation of the horizontal kinetic energy. In particular, when the eddy coefficients are horizontally uniform, it ensures a complete separation of vorticity and horizontal divergence fields, so that diffusion (dissipation) of vorticity (enstrophy) does not generate horizontal divergence (variance of the horizontal divergence) and vice versa.

These properties of the horizontal diffusion operator are a direct consequence of properties (4.9) and (4.10). When the vertical curl of the horizontal diffusion of momentum (discrete sense) is taken, the term associated with the horizontal gradient of the divergence is locally zero.

Conservation of Potential Vorticity

The lateral momentum diffusion term conserves the potential vorticity :

$$\int \limits_D \frac{1} {e_3 } \textbf{k} \cdot \nabla \times \Bi... ...ight) - \nabla_h \times \left( A^{ lm}\;\zeta \; \textbf{k} \right) \Bigr]\;dv$$

$$= \int \limits_D -\frac{1} {e_3 } \textbf{k} \cdot \nabla \times \Bigl[ \nabla_h \times \left( A^{ lm}\;\zeta \; \textbf{k} \right) \Bigr]\;dv$$

$$\equiv \sum\limits_{i,j} \left\{ \delta_{i+1/2} \left[ \frac {e_{2v}} {e... ..._{2u} e_{3u}} \delta_j \left[ A_f^{ lm} e_{3f} \zeta \right] \right] \right\}$$
Using (4.11), it follows:

$$\equiv \sum\limits_{i,j,k} - \left\{ \frac{e_{2v}} {e_{1v} e_{3v}} \de... ...f^{ lm} e_{3f} \zeta \right]\;\delta_j \left[ 1\right] \right\} \quad \equiv 0$$

Dissipation of Horizontal Kinetic Energy

The lateral momentum diffusion term dissipates the horizontal kinetic energy:

$$\begin{split}\int_D \textbf{U}_h \cdot \left[ \nabla_h \right... ...,\zeta^2 \;e_{1f } e_{2f } e_{3f} \quad \leq 0 \end{split}$$

Dissipation of Enstrophy

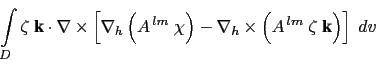The lateral momentum diffusion term dissipates the enstrophy when the eddy coefficients are horizontally uniform:

$$\int\limits_D \zeta \; \textbf{k} \cdot \nabla \times \left[ \nab... ...ght) - \nabla_h \times \left( A^{ lm}\;\zeta \; \textbf{k} \right) \right]\;dv$$

$$\quad = A^{ lm} \int \limits_D \zeta \textbf{k} \cdot \nabla \times \left[ \nabla_h \times \left( \zeta \; \textbf{k} \right) \right]\;dv$$

$$\quad \equiv A^{ lm} \sum\limits_{i,j,k} \zeta \;e_{3f} \left\{ ... ...{e_{1u}} {e_{2u} e_{3u}} \delta_j \left[ e_{3f} \zeta \right] \right] \right\}$$
Using (4.11), it follows:

$$\quad \equiv - A^{ lm} \sum\limits_{i,j,k} \left\{ \left( \frac{... ...3u}} \delta_j \left[ e_{3f} \zeta \right] \right)^2 b_u \right\} \quad \leq \;0$$

Conservation of Horizontal Divergence

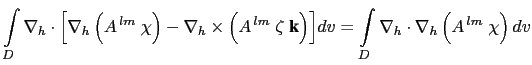When the horizontal divergence of the horizontal diffusion of momentum (discrete sense) is taken, the term associated with the vertical curl of the vorticity is zero locally, due to (4.10). The resulting term conserves the $\chi$ and dissipates $\chi^2$ when the eddy coefficients are horizontally uniform.

$$\int\limits_D \nabla_h \cdot \Bigl[ \nabla_h \left( A^{ lm}\;\ch... ...gr] dv = \int\limits_D \nabla_h \cdot \nabla_h \left( A^{ lm}\;\chi \right) dv$$

$$\equiv \sum\limits_{i,j,k} \left\{ \delta_i \left[ A_u^{ lm} \fr... ...ac{e_{1v} e_{3v}} {e_{2v}} \delta_{j+1/2} \left[ \chi \right] \right] \right\}$$
Using (4.11), it follows:

$$\equiv \sum\limits_{i,j,k} - \left\{ \frac{e_{2u} e_{3u}} {e_{1u... .../2} \left[ \chi \right] \delta_{j+1/2} \left[ 1 \right] \right\} \quad \equiv 0$$

Dissipation of Horizontal Divergence Variance

$$\int\limits_D \chi \;\nabla_h \cdot \left[ \nabla_h \left( A^{ l... ... A^{ lm} \int\limits_D \chi \;\nabla_h \cdot \nabla_h \left( \chi \right)\; dv$$

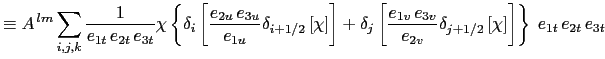$$\equiv A^{ lm} \sum\limits_{i,j,k} \frac{1} {e_{1t} e_{2t} e_{... ...} \delta_{j+1/2} \left[ \chi \right] \right] \right\} \; e_{1t} e_{2t} e_{3t}$$
Using (4.11), it turns out to be:

$$\equiv - A^{ lm} \sum\limits_{i,j,k} \left\{ \left( \frac{1} {e_... ...{e_{2v}} \delta_{j+1/2} \left[ \chi \right] \right)^2 b_v \right\} \quad \leq 0$$