Next: Output and Diagnostics (IOM, Up: Vertical Ocean Physics (ZDF) Previous: Tidal Mixing (key_ zdftmx) Contents Index
!-----------------------------------------------------------------------
&namzdf_tmx_new ! new tidal mixing parameterization ("key_zdftmx_new")
!-----------------------------------------------------------------------
nn_zpyc = 1 ! pycnocline-intensified dissipation scales as N (=1) or N^2 (=2)
ln_mevar = .true. ! variable (T) or constant (F) mixing efficiency
ln_tsdiff = .true. ! account for differential T/S mixing (T) or not (F)
/
The parameterization of mixing induced by breaking internal waves is a generalization
of the approach originally proposed by St. Laurent et al. [2002].
A three-dimensional field of internal wave energy dissipation
![]() is first constructed,
and the resulting diffusivity is obtained as
is first constructed,
and the resulting diffusivity is obtained as
In addition to the mixing efficiency, the ratio of salt to heat diffusivities can chosen to vary
as a function of ![]() by setting the ln_tsdiff parameter to true, a recommended choice).
This parameterization of differential mixing, due to Jackson and Rehmann [2014],
is implemented as in de Lavergne et al. [2016].
by setting the ln_tsdiff parameter to true, a recommended choice).
This parameterization of differential mixing, due to Jackson and Rehmann [2014],
is implemented as in de Lavergne et al. [2016].
The three-dimensional distribution of the energy available for mixing,
![]() , is constructed
from three static maps of column-integrated internal wave energy dissipation,
, is constructed
from three static maps of column-integrated internal wave energy dissipation,
![]() ,
,
![]() , and
, and
![]() , combined to three corresponding vertical structures
(de Lavergne et al., in prep):
, combined to three corresponding vertical structures
(de Lavergne et al., in prep):
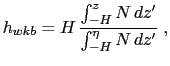 |
Gurvan Madec and the NEMO Team
NEMO European Consortium2017-02-17