Lateral/Vertical Momentum Diffusive Operators

The second order momentum diffusion operator (Laplacian) in the $z$-coordinate is found by applying (2.7e), the expression for the Laplacian of a vector, to the horizontal velocity vector :

$$\Delta {\textbf{U}}_h =\nabla \left( {\nabla \cdot {\textbf{U}}_h } \right)- \nabla \times \left( {\nabla \times {\textbf{U}}_h } \right)$$

$$=\left( {{\begin{array}{*{20}c} {\frac{1}{e_1 }\frac{\partial \ch... ...rac{\partial v}{\partial k}} \right)} \right]} \hfill \end{array} }} \right)$$

$$=\left( {{\begin{array}{*{20}c} {\frac{1}{e_1 }\frac{\partial \ch... ...t( {e_1 v} \right)}{\partial j\partial k}} \right)} \end{array} }} \right)$$

Using (2.7b), the definition of the horizontal divergence, the third componant of the second vector is obviously zero and thus :

$$\Delta {\textbf{U}}_h = \nabla _h \left( \chi \right) - \nabla _h... ...} \left( {\frac {1}{e_3 } \frac{\partial {\textbf{ U}}_h }{\partial k}} \right)$$

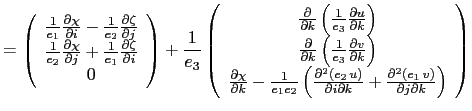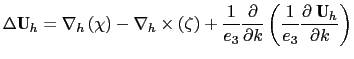Note that this operator ensures a full separation between the vorticity and horizontal divergence fields (see Appendix C). It is only equal to a Laplacian applied to each component in Cartesian coordinates, not on the sphere.

The horizontal/vertical second order (Laplacian type) operator used to diffuse horizontal momentum in the $z$-coordinate therefore takes the following form :

$${\textbf{D}}^{\textbf{U}} = \nabla _h \left( {A^{lm}\;\chi } \rig... ...\frac{A^{vm}\;}{e_3 } \frac{\partial {\rm {\bf U}}_h }{\partial k}} \right)$$ (B.7)

that is, in expanded form:

$$D^{\textbf{U}}_u = \frac{1}{e_1} \frac{\partial \left( {A^{lm}\chi } \right)}{\par... ...A^{lm}\zeta } \right)}{\partial j} +\frac{1}{e_3} \frac{\partial u}{\partial k}$$

$$D^{\textbf{U}}_v = \frac{1}{e_2 }\frac{\partial \left( {A^{lm}\chi } \right)}{\par... ...A^{lm}\zeta } \right)}{\partial i} +\frac{1}{e_3} \frac{\partial v}{\partial k}$$

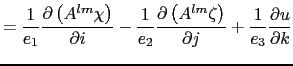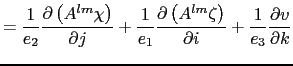Note Bene: introducing a rotation in (B.8) does not lead to a useful expression for the iso/diapycnal Laplacian operator in the $z$-coordinate. Similarly, we did not found an expression of practical use for the geopotential horizontal/vertical Laplacian operator in the $s$-coordinate. Generally, (B.8) is used in both $z$- and $s$-coordinate systems, that is a Laplacian diffusion is applied on momentum along the coordinate directions.