Next: Configurations Up: Miscellaneous Topics Previous: Model Optimisation, Control Print Contents Index
!-----------------------------------------------------------------------
&namsol ! elliptic solver / island / free surface
!-----------------------------------------------------------------------
nn_solv = 1 ! elliptic solver: =1 preconditioned conjugate gradient (pcg)
! =2 successive-over-relaxation (sor)
nn_sol_arp = 0 ! absolute/relative (0/1) precision convergence test
rn_eps = 1.e-6 ! absolute precision of the solver
nn_nmin = 300 ! minimum of iterations for the SOR solver
nn_nmax = 800 ! maximum of iterations for the SOR solver
nn_nmod = 10 ! frequency of test for the SOR solver
rn_resmax = 1.e-10 ! absolute precision for the SOR solver
rn_sor = 1.92 ! optimal coefficient for SOR solver (to be adjusted with the domain)
/
When the filtered sea surface height option is used, the surface pressure gradient is
computed in dynspg_flt.F90. The force added in the momentum equation is solved implicitely.
It is thus solution of an elliptic equation (![[*]](crossref.png) ) for which two solvers are available:
a Successive-Over-Relaxation scheme (SOR) and a preconditioned conjugate gradient
scheme(PCG) [Madec, 1990, Madec et al., 1988]. The solver is selected trough the
the value of nn_solv namsol namelist variable.
) for which two solvers are available:
a Successive-Over-Relaxation scheme (SOR) and a preconditioned conjugate gradient
scheme(PCG) [Madec, 1990, Madec et al., 1988]. The solver is selected trough the
the value of nn_solv namsol namelist variable.
The PCG is a very efficient method for solving elliptic equations on vector computers. It is a fast and rather easy method to use; which are attractive features for a large number of ocean situations (variable bottom topography, complex coastal geometry, variable grid spacing, open or cyclic boundaries, etc ...). It does not require a search for an optimal parameter as in the SOR method. However, the SOR has been retained because it is a linear solver, which is a very useful property when using the adjoint model of NEMO.
At each time step, the time derivative of the sea surface height at time step ![]() (or equivalently the divergence of the after barotropic transport) that appears
in the filtering forced is the solution of the elliptic equation obtained from the horizontal
divergence of the vertical summation of (
(or equivalently the divergence of the after barotropic transport) that appears
in the filtering forced is the solution of the elliptic equation obtained from the horizontal
divergence of the vertical summation of (![[*]](crossref.png) ).
Introducing the following coefficients:
).
Introducing the following coefficients:
Note that in the linear free surface case, the depth that appears in (15.2) does not vary with time, and thus the matrix can be computed once for all. In non-linear free surface (key_ vvl defined) the matrix have to be updated at each time step.
Let us introduce the four cardinal coefficients:
initialisation (evaluate a first guess from previous time step computations)
| (15.5) |
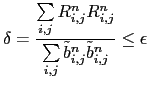 |
(15.7) |
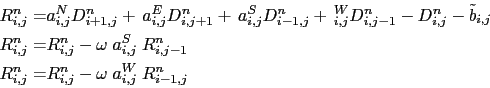 |
(15.8) |
Another technique have been chosen, the so-called red-black SOR. It consist in solving successively
(15.6) for odd and even grid points. It also slightly reduced the convergence rate
but allows the vectorisation. In addition, and this is the reason why it has been chosen, it is able to handle the north fold boundary condition used in ORCA configuration (![]() tri-polar global ocean mesh).
tri-polar global ocean mesh).
The SOR method is very flexible and can be used under a wide range of conditions, including irregular boundaries, interior boundary points, etc. Proofs of convergence, etc. may be found in the standard numerical methods texts for partial differential equations.
A is a definite positive symmetric matrix, thus solving the linear system (15.3) is equivalent to the minimisation of a quadratic functional:
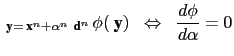 |
initialisation :
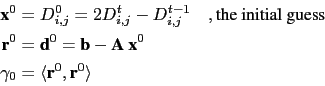 |
iteration ![]() from
from ![]() until convergence, do :
until convergence, do :
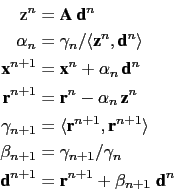 |
(15.9) |
The convergence test is:
| (15.10) |
It can be demonstrated that the above algorithm is optimal, provides the exact
solution in a number of iterations equal to the size of the matrix, and that
the convergence rate is faster as the matrix is closer to the identity matrix,
![]() its eigenvalues are closer to 1. Therefore, it is more efficient to solve
a better conditioned system which has the same solution. For that purpose,
we introduce a preconditioning matrix Q which is an approximation
of A but much easier to invert than A, and solve the system:
its eigenvalues are closer to 1. Therefore, it is more efficient to solve
a better conditioned system which has the same solution. For that purpose,
we introduce a preconditioning matrix Q which is an approximation
of A but much easier to invert than A, and solve the system:
The same algorithm can be used to solve (15.11) if instead of the
canonical dot product the following one is used:
![]() , and
if
, and
if
![]() and
and
![]() are substituted to b and A [Madec et al., 1988].
In NEMO, Q is chosen as the diagonal of A, i.e. the simplest form for
Q so that it can be easily inverted. In this case, the discrete formulation of
(15.11) is in fact given by (15.4) and thus the matrix and
right hand side are computed independently from the solver used.
are substituted to b and A [Madec et al., 1988].
In NEMO, Q is chosen as the diagonal of A, i.e. the simplest form for
Q so that it can be easily inverted. In this case, the discrete formulation of
(15.11) is in fact given by (15.4) and thus the matrix and
right hand side are computed independently from the solver used.
Gurvan Madec and the NEMO Team
NEMO European Consortium2017-02-17