Divergence damping initialisation
The velocity increments may be initialized by the iterative application of
a divergence damping operator. In iteration step 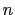 new estimates of
velocity increments
new estimates of
velocity increments 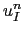 and
and 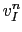 are updated by:
are updated by:
where
![$\displaystyle \chi^{n-1}_I = \frac{1}{e_{1t} e_{2t} e_{3t} } \left( {\delta _...
...n-1}_I} \right] +\delta _j \left[ {e_{1v} e_{3v} v^{n-1}_I} \right]} \right).$](img1303.png) |
(13.5) |
By the application of (13.4) and (13.4) the divergence is filtered
in each iteration, and the vorticity is left unchanged. In the presence of coastal boundaries
with zero velocity increments perpendicular to the coast the divergence is strongly damped.
This type of the initialisation reduces the vertical velocity magnitude and alleviates the
problem of the excessive unphysical vertical mixing in the first steps of the model
integration [Dobricic et al., 2007, Talagrand, 1972]. Diffusion coefficients are defined as
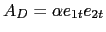 , where
, where
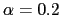 . The divergence damping is activated by
assigning to nn_divdmp in the nam_asminc namelist a value greater than zero.
By choosing this value to be of the order of 100 the increments in the vertical velocity will
be significantly reduced.
. The divergence damping is activated by
assigning to nn_divdmp in the nam_asminc namelist a value greater than zero.
By choosing this value to be of the order of 100 the increments in the vertical velocity will
be significantly reduced.
Gurvan Madec and the NEMO Team
NEMO European Consortium2017-02-17
![]() new estimates of
velocity increments
new estimates of
velocity increments ![]() and
and ![]() are updated by:
are updated by: